Cuando se mezclan 2 gases en un volumen definido a la misma presion y temperatura, deberia hacer que la entropia aumente. Es el resultado de la suma de 2 entriopias. Gibbs presento una paradoja cuando se mezclaban 2 gases. Si los gases son los mismos no se calcularia la entripia extra por que no hay mezcla en si son el mismo gas.
Aqui una explicacion matematica:
Podemos escribir la entropía en notación más compacta como
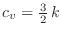
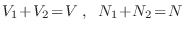 0 \;. $">
0 \;. $">![$\displaystyle \fbox{ $\displaystyle S = \frac32 Nk\left(\frac53 + \ln\fr... ...ht) + Nk \ln\left(\frac VN u^{3/2}\right) \rule[-1.75em]{0em}{4em} $ } $](http://www.famaf.unc.edu.ar/~gcas/termo2/clases/img487.png)
la fórmula de Stirling es una aproximación para factoriales grandes. Por lo tanto se sugiere que las partículas son indistinguibles, existen 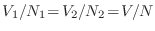 permutaciones que proveen el mismo estado, aunque está claro que dentro de la teoría clásica todas las partículas son distinguibles. La verdadera respuesta es en realidad provista por la cuántica, en el marco de la llamada ``segunda cuantización'': como veremos más adelante, para describir
permutaciones que proveen el mismo estado, aunque está claro que dentro de la teoría clásica todas las partículas son distinguibles. La verdadera respuesta es en realidad provista por la cuántica, en el marco de la llamada ``segunda cuantización'': como veremos más adelante, para describir 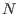 partículas idénticas, las funciones de onda conjuntas deben ser simétricas o antisimétricas ante permutaciones de partículas, y cuando las condiciones indican que la descripción debe coincidir con el enfoque clásico, se vé que entonces ambas formulaciones concuerdan gracias a este denominador
partículas idénticas, las funciones de onda conjuntas deben ser simétricas o antisimétricas ante permutaciones de partículas, y cuando las condiciones indican que la descripción debe coincidir con el enfoque clásico, se vé que entonces ambas formulaciones concuerdan gracias a este denominador 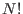 .
.
Fuentes:
Jaja, casi ni se ve, pero lo redactado me para muy bien investigado...
ResponderEliminarSaludos
Hola,
ResponderEliminarMe parecio muy interesante tu informacion, he aprendido algo nuevo
Saludos